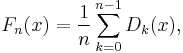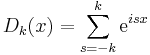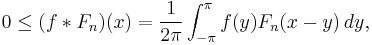Fejér kernel

In mathematics, the Fejér kernel is used to express the effect of Cesàro summation on Fourier series. It is a non-negative kernel, giving rise to an approximate identity.

The Fejér kernel is defined as

$F_n(x) = \frac{1}{n} \sum_{k=0}^{n-1}D_k(x),$

where

$D_k(x)=\sum_{s=-k}^k {\rm e}^{isx}$

is the kth order Dirichlet kernel. It can also be written in a closed form as

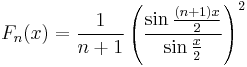$F_n(x) = \frac{1}{n%2B1} \left(\frac{\sin \frac{(n%2B1) x}{2}}{\sin \frac{x}{2}}\right)^2$ ,

where this expression is defined.^[1] It is named after the Hungarian mathematician Lipót Fejér (1880–1959).

The important property of the Fejér kernel is 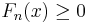$F_n(x) \ge 0$ . The convolution F_n is positive: for 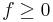$f \ge 0$ of period 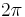$2 \pi$ it satisfies

$0 \le (f*F_n)(x)=\frac{1}{2\pi}\int_{-\pi}^\pi f(y) F_n(x-y)\,dy,$

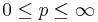
$\|F_n*f \|_{L^p([-\pi, \pi])} \le \|f\|_{L^p([-\pi, \pi])}$ for every $0 \le p \le \infty$

or continuous function $f$ ; moreover,

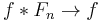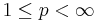$f*F_n \rightarrow f$ for every $f \in L^p([-\pi, \pi])$ ( $1 \le p < \infty$ )

or continuous function $f$ . Indeed, if $f$ is continuous, then the convergence is uniform.

References

^ Hoffman, Kenneth (1988). Banach Spaces of Analytic Functions. Dover. p. 17. ISBN 0-486-45874-1.